Thales Theorem

Created Thursday 05 December 2024

To find the centre of a circle using a 'square'

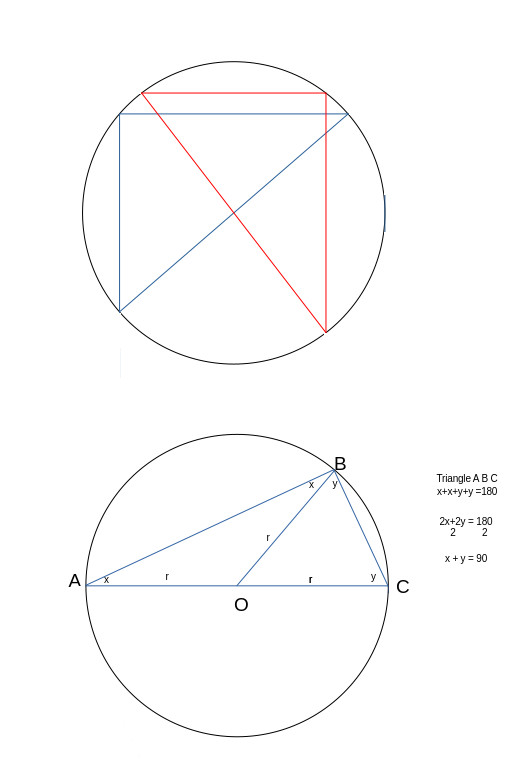
Thales's theorem can also be used to find the centre of a circle using an object with a right angle, such as a set square or rectangular sheet of paper larger than the circle.
The angle is placed anywhere on its circumference (Blue). The intersections of the two sides with the circumference define a diameter. Repeating this with a different set of intersections yields another diameter (Red).
The centre is at the intersection of the diameters.

In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ∠ ABC is a right angle.
Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements.
It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

The following facts are used: the sum of the angles in a triangle is equal to 180° and the base angles of an isosceles triangle are equal.
A B O and B C O are isosceles triangles.

If you have a comment or suggestion, please use the form on the contact page.